SSC Maths Previous Public Examination Questions from March 2015 To June 2023
1. Real Numbers
1 Mark
- Insert 4 rational numbers between 3/4 and 1 without using formula a + b/ 2 (M’15)
- The prime factorization of a natural number(n) is 23 x 32 x 52 x 7. How many consecutive zeroes will it have at the end of it? justify your answer. (J’15)
- Find the value of log5 125 (M’16)
- Write any two irrational numbers lying between 3 and 4. (J’16)
- Find the value of log√2 256. (M’17)
- Find the HCF and LCM of 90, 144 by prime factorization method ( J’17)
- Is log3 81 rational or irrational? Justify your answer. ( J’17)
- Expand log10 385. (M’18)
- Find the value of log√2 128 . ( J’18 )
- Find the HCF of 24 and 33 by using division algorithm. (M’19)
- Ramu says, “If log10 x = 0, value of x =0”. Do you agree with him? Give reason. (J’19)
- Expand log a3b2c5 (May 2022)
- Expand log 32/81 (Aug. 2022
- Find the mean of the factors of 24.(Jun’23)
2 Marks
- Write any three numbers of two digits. Find the L.C.M. and H.C.F. for the above numbers by the “Prime factorization method” . (M’15)
- Give an example for each of the following
- i)The product of two rational numbers is a rational number.
- ii) The product of two irrational numbers is an irrational number. (M’15)
- state with reasons which of the following are rational numbers and which are irrational numbers. (i) √225x√4 (ii) 6√50 + 8√125 . (J’15)
- If x2 + y2 = 7xy then show that 2 log(x + y) = logx + logy + 2log 3 (M’16)
- Express 2016 as product of prime factor. ( J’16)
- Write any two three-digit numbers. Find their L.C.M. and G.C.D. by prime factorization method. (M’17)
- Prove that 2 + √3 is irrational. ( J’17)
- Lalitha says that HCF and LCM of the numbers 80 and 60 are 20 and 120 respectively. Do you agree with her ? Justify. ( J’18 )
- If x2 + y2 = 10xy, prove that 2 log (x + y) = log x + logy + 2log 2 + log 3. (J’19, Apr’23)
- If 2304 = 2x × 3y then find the value of log y x. (Jun’23)
4 MARKS
1. Prove that 3 + 2√5 is an irrational number. (M’15)
2. Expand log(1125/32) (J’15)
3. Express the numbers 6825 and 3825 as a product of its prime factors. Find the HCF and LCM of the above numbers by using their products of prime factors. Justify your answer. (J’15)
4. Use Euclid’s division Lemma to show that the cube of any positive integer is of the form 7m or 7m + 1 or 7m + 6. (M’16)
5.Prove that √2 − 3√5 is an irrational number. (M’16)
6. Use Euclid’s division lemma, show that the cube of any positive integer is of the form 3p or 3p + 1or 3p + 2 for any integer ‘p’. (J’16)
7. Prove that √3 – √5 is an irrational number. (J’16)
8. Use Euclid’s division lemma to show that the square of any positive integer is of the form 5n or 5n +1 or 5n + 4 where n is a whole number. (M’17) & (J’19)
9. If x2 + y2 = 27xy, then show that log (x – y)/5 = 1/2[logx + logy] ( J’17)
10. Show that cube of any positive integer will be in the form of 8m or 8m +1 or 8m + 3 or 8m + 5 or 8m + 7, where m is a whole number. (M’18)
11. Prove that √3 + √5 is an irrational number. (M’18) 1
2. Prove that √2 + √11 is an irrational number. ( J’18 )
13. Prove that √2 + √7 is an irrational number. (M’19)
14. Use division algorithm to show that the square of any positive integer is of the form 5mor 5m +1 or 5m + 4 where m is a whole number. (J’19)
15.Show that √5 − √3 is an irrational number. (J’19)
16.Prove that √5 + √7 is an irrational number. (May 2022)
17. Prove that √3 + √7 is an irrational number. (Aug 2022)
18. Prove that 2√3 + √5 is an irrational number. (Apr’23)
2.SETS
1 MARK
- If A ={x :x∈ N and x< 20} and B = { x : x∈ N and x ≤ 5 } then write the set A – B in the set builder form. (M’15)
- “B is a set of all months in a year having 30 days”. Write the above set in the roster form.
3. If A – B = {3,4, 5}, B – A {1, 8, 9} and A∩B = {6, 7}, then find A∪B. (J’15)(J’15)
4. If A = {1, 1/4, 1/9, 1/16, 1/25 } , then write A In set builder form. (M’16)
5. A = {x: x∈ N, x is a composite number and x < 13}. Write set A In the roster form. (J’16)
6. Represent A∩B through Venn diagram, Where A = {1, 4, 6, 9,10} and B = {x / x is a perfect square less than 25}. (M’17)
7. If A = {1, 2, 3, 4, 5 }, b = { 3, 4, 5, 6 }, Find A∩B. ( J’17)
8. Give one example each for a finite set and an infinite set. (M’18)
9. List all the subsets of the set A = { x, y , z } ( J’18 )
10. If A = {x: x is a factor of 24}, then find n(A). (M’19)
11. If A = {1, 2, 3}, B = {3, 4, 5 } Then find A – B and B – A (J’19)
12. A = {x : x is a factor of 8}, B = {x : x is a factor of 36}. Is A ⸦ B? Justify. (Jun’23)
2 MARKS
- If A = {x : x ∈ N and x < 6} and B = { x : x ∈ N and 3 < x < 8 } then Show that A – B ≠ B – A with the help of Venn diagram. (M’15)
- Answer the following questions and justify your answers. A ={x :x ∈ N, x < 2015 }, is it a finite set or infinite set ? B ={x : x + 5 = 5 } is it a null set or a Universal set ? (J’15)
- A = { x : x ∈ N, and x is a factor of 30} ; B = {x : x ∈ N, and x is a prime factor of 30} draw Venn diagram for A∪B ( J’16)
- If A = { x : x ∈ N, x < 10 }, B = { x : x is a prime number and x x < 10 }, Then show that A – B ≠ B – A with the help of Venn diagram. ( J’17)
- If A ={1, 2, 3, 4}, B = {2, 4, 6, 8, 10}, then represent the Venn diagram of A – B. (J’18)
6. If µ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = { 2, 3, 5, 8} and B = {0, 3, 5, 7, 10}. Then represent A⋂B in the Venn diagram. (M’19)
7. If A ={ x : x is a factor of 12} and B = {x: x is a factor of 6} then find A∪B and A∩B. (J’19)
8. If A = {1, 2, 3, 4, 5} and B = {2, 4, 6, 8}. Then show that n(A ∪B) = n(A) + n(B) – n(A∩ B). (May 2022)
9. If A = { 4, 8, 12, 16, 20 }, B = { 6, 12, 18, 24, 30 }, then show that n(A∪B) = n(A) + n(B) – n(A∩B) . (AUG 2022)
10. From the given Venn diagram show that n (A ∪ B) = n (A) + n (B) – n (A ∩ B) .
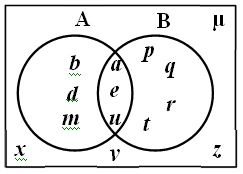
4 Marks
- X is a set of factors of 24 and Y is a set of factors of 36, then find sets X∪Y and X∩Y by using Venn diagram and comment on the answer. (M’16)
- A = {x : x ∈ N and x is a multiple of 4}; B = {x : x ∈ N and x is a multiple of 6 C = {x : x ∈ N and x is a multiple LCM of 4 and 6} . Find A∩B. How can you relate the sets A∩B and C. (J’16)
- From the following Venn diagram, write the elements of sets A and B. And verify n(A∪B) + n(A∩B) = n(A) + n(B). (M’17)
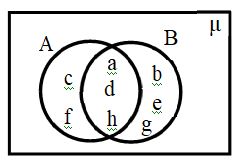
- 4. Using the Venn diagram, verify n (A∪B ) = n(A) + n(B) – n(A∩B). ( J’17)
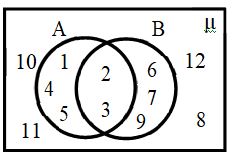
- 5. A = { x : x is a perfect square, x < 50, x ∈ N }, B = { x : x = 8m + 1, where m ∈ W, x < 50, x ∈ N}. Find A∩B and display it with Venn diagram. (M’18)
- 6. If A = {x : x is a prime and x < 10 },B = { x : x is a factor of 6 }, then find A∩B, A∪B and A – B. ( J’18 )
- 7. If A = {x : 2x + 1, x∈ N, x ≤ 5 }, B = {x : x is a composite number, x ≤ 12}, then show that (A⋃B) – (A⋂B) = (A – B) ⋃ (B – A )(M’19)
- 8. If A={x : x is a prime less than 20} and B = {x : x is whole number less than 10} then verify n(A∪B) = n(A) +n(B) – n(A∩B). (J’19)
- 9. From the given Venn diagram, write the sets A ∪ B, A ∩ B, A – B and B – A. (May 2022
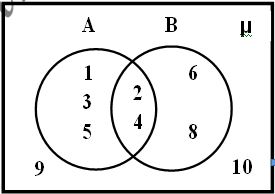
- 10 From the given when diagram,write the sets A∪B, A∩B, A – B and B – A. (AUG.2022)
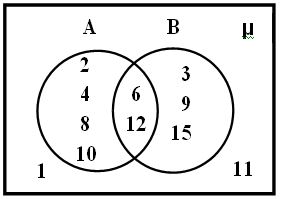
- Set A = {F,L, W,O} Which of the following is not a set builder form for set A (J’15)
- A) {x : x is a letter from the world FOLLOW}
- B) { x : x is a letter from the world FLOW}
- C) { x : x is a letter from the world WOLF}
- D) { x : x is a letter from the world SLOW}
2. If the union of two sets is one of the set itself, then the relation between in the two sets is (J’15)
- A) One set is a subset of other set B) Equal number of elements of both the sets
- C) Disjoint sets D) Empty sets
- 3. Which one of the following is the example of finite set? (M’16)
- A) {x / x∈ N and x2 = 9} B) Set of all multiples of even prime numbers
- C) Set of rational numbers between 2 and 3.. D) Set of all odd prime numbers.
3.POLYNOMIALS
1 MARK
- If x ≠ – 1, then find the quotient of x5 + x4 + x3 + x2 / x3 + x2 + x + 1 (M’15)
- “We can write a trinomial having degree 7”.Justify the above statement by giving one example. (M’15)
- Write an example for a quadratic Polynomial that has no zeros. (M’16)
- If p(x) = x3 – 3x2+ 2x – 3 is a polynomial, then find the value of p(1). (J’16)
- Srikar says that the order of the polynomial (x2 – 5)(x3+1) is 6. Do you agree with him?
- Find zeros of the polynomial P(x) = x2 – 4. (J’17)
- Verify the relation between zeros and coefficients of the quadratic polynomial is x2 – 4. (M’18)
- Weather 1/2 and 1 all zeros of the polynomial p(x) = 2x2 – 3x + 1 or not? Justify. (J’18)
- If P(x) = x4 + 1, then find P(2) – P(-2). (M’19)
- – 3, 0 and 2 are the zeroes of the polynomial p(x) = x3 + (a – 1) x2 + bx + c Find a and c. (J’19)
- Write any two linear polynomials having one term under three terms. (J’19)
- If p(x) = x2 + 3x + 4, then find the values of p(0) and p(1). (May 2022)
- If p(x) = 2x2 + 5x – 7, then find the value of p(0) and p(1). (Aug 2022)
2 MARKS
- For what value of k, – 4 is a zero of the polynomial x2 – x – (2k + 2). (J’15).
- Use the table given below to draw the graph. Use the graph drawn to find the values of a and b. (J’15)
| x | -2 | 0 | 2 | 1 | b |
| y | -3 | 1 | a | 3 | -7 |
- 3. Length of a rectangle is 5 units more than its breadth. Express its perimeter in polynomial form.
- 4. Show that 2 and − 1/3 are zeros of the polynomial 3x2 – 5x – 2 (J’16)
- 5. Which of √2 and 2 is a zero of the polynomial p(x) = x3–2x? Why? (M’17)
- 6. Divide x3 – 3x2 + 5x –3 by x2 – 2. And verify the division lemma. (J’17)
- 7. Complete the following table for the polynomial y = p(x) = x3– 2x + 3. (M’18)
| x | –1 | 0 | 1 | 2 |
| x3 | ||||
| – 2x | ||||
| 3 | ||||
| y | ||||
| (x, y) |
- 8. If one of the zeros of the cubic polynomial p(x) = ax3 + bx2 + cx + d is zero, then find the product of other two zeros of p(x). (a ≠ 0). (J’18)
- 9. Divide x3 – 4x2 + 5x – 2 by x – 2. (M’19)
4 MARKS
- Lakshmi does not want to disclose the length, breath the height of a cuboid of her project. she has constructed a polynomial x3 – 6x2 + 11x – 6 by taking the values of length, breath and height as its zeros. Can you open the secret [ i.e., find the measures of length, breath on the height?(M’15)
- Draw the graph for the polynomial p(x) = x2 + 3x– 4 and find its zeroes from the graph. (M’15, J’19)
- Draw the graph of the polynomial p(x) = 3x2 + 2x – 1 on the graph paper. Find its zeros from the graph. (J’15)
- Draw the graph for the polynomial p(x) = x2 – 3x + 2 and find the zeroes from the graph. (M’16)
- Draw the graph of the polynomial p(x) = x2 – 5x + 4 on the graph paper. Find its zeros from the graph. (J’16)
- On dividing by x3 – 3x2 + 5x – 7 by x2 – 2x + 4, If the remainder is in the form of Ax + B, find the values of A and B. (J’16).
- Divide 3x4 – 5x3 + 4x2 + 3x – 5 by x2 – 3 and verify the division algorithm. (M’17)
- The perimeter of a right-angle triangle is 60 cm and its hypotenuse is 25 cm. Then find the remaining two sides. (M’17)
- Draw the graph of the polynomial p(x) = x2– 5x + 6 and find the zeros from the graph. (M’17)
- Draw the graph of p(x) = x2 – 2x – 8 and find the zeros of the polynomial from it. ( J’17)
- Total number of pencils required are given by 4x4 + 2x3 – 2x2 + 62x – 66. If each box contains x2 + 2x – 3 pencils, then find the number of boxes to be purchased. (M’18)
- Draw the graph of the polynomial p (x) = x2 + x – 2 on the graph paper. Find its zeroes from the graph. ( J’18 )
- Draw the graph of the polynomial p(x) = x2 – 7x + 12, then find its zeroes from the graph. (M’19)
- Draw the graph of the polynomial p(x) = x2 + 2x – 3 and find the zeroes of the polynomial from the graph. (May 2022, Jun’23)
- Draw the graph of the quadratic polynomial p(x)= x2 – 4x + 3 and find the zeroes of the polynomial from the graph. (Apr’23)
- Draw the graph of the polynomial p(x) = x2 – x – 2 and find the zeros of the polynomial from the graph. (Aug 2022)
4.Pair of Linear equations in two VariabLes
1 Marks
- For what value of k, the following system of equations has a unique solution. x – ky = 2 and 3x + 2y = – 5 (M’15)
- For what values of m, the pair of equations3x + my= 10 and 9x + 12y=30 have a unique solution. (M’16)
- In a rectangle ABCD, AB = x + y, BC = x – y, CD = 9 and AD = 3. Find the values of x and y. (J’16)
- Show that the pair Linear Equations 7x + y = 10 and x + 7y = 10 are consultant. (M’17)
- Write the Condition for the pair of linear equations in two variables to be parallel lines. ( J’17)
- If x = a and y = b is solution for the pair of equations x– y = 2 and x + y = 4, then find the values of a and b. (M’18)
- Whether the following pair of Linear Equations are parallel? Justify. 6x – 4y + 10 = 0, 3x – 2y + 6 = 0. ( J’18 )
- For what value of ‘t’ the following pair of linear equations has a no solution? 2x – ty = 5 and 3x + 2y = 11. (M’19)
- The solution of the linear equation x + y = 5 are (1, 4), (2, 3) and (3, 2). The solution of another linear equation x – y = 1 are (3, 2), (2, 1) and (5, 4). Plot these points on a graph sheet and draw lines. (May 2022)
- The solutions of the linear equation x + y = 8 are (1,8), (2, 6) and (3, 5). The solutions of another linear equation 3x + 3y =12 are (1, 3), (3,1) and (9, 4). flat these points on a graph sheet and draw lines.
- If the pair of linear equations 6x – 4y + 10 = 0 and 3x + ky + 6 = 0 represents parallel lines graphically, then find the value of ‘k’. (Jun’23)
2 Marks
- If we multiply or divide both sides of a linear equation by a non- zero number, then the roots of that linear equation will remain the same’. is it true? If so, justify with an example. (M’15)
- If the present ages of A and B are in ratio of 9 : 4 and after 7 years the ratio of the ages will be 5 : 3 then find their present ages. (J’15)
- Solve the following pair of linear equations by substitution method. 2x – 3y = 19 and 3x – 2y = 21 (M’16)
- If the measure of angles of a triangle are x0, y0 and 400, and difference between the measures of angles x0and y0 is 300, then find values of x0 and y0. ( J’16)
- Given the linear equation 3x + 4y = 11, write linear equations in two variables such that their geometrical representations form parallel lines and intersecting lines. (M’18)
- Solve the pair of linear equations 2x + 3y = 8 and x + 2y = 5 by Elimination method. (M’19)
- For what values of m the following mx + 4y = 10 and 9x + 12y = 30 system of equations will have no solution? Why? (J’19).
- Solve 2x + y = 5 and 5x + 3y = 11. (May 2022)
- Solve 3x + 2y = 11 and 2x + 3y = 4. (Aug 2022)
4 Marks
- Draw a graph for the following pair of linear equations in two variables and find their solution from the graph 2x + y = 5 and 3x – 2y = 4 (M’15)
- Draw the graphs of the following equations 3x – y – 2 = 0 and 2x + y – 8 = 0 on the graph paper.
- i) Write down the co-ordinates of the point of intersection of the equations.
- ii) Find the area of the triangle formed by the lines and the X-axis. (J’15)
- Draw the graph for the equations 2x – 3y = 5 and 4x – 6y = 15 on the graph paper and check whether they are consistent or not. (J’15)
- Draw the graph for the following pair of linear equations in two variables and find their solution from the graph. 3x– 2y = 2 and 2x + y = 6 (M’16)
- Draw the graph for the equations 2x – y – 4 = 0 and x + y = 0 on the graph paper and check whether they are consistent or not. (J’16)
- Draw the graph of 2x + y = 6 and 2x – y + 2 = 0 and find the solution from the graph. (M’17)
- Show that the following pair of equations are consistent and show them graphically
- x + 3y = 6 and 2x– 3y = 12 (J’17)
- Solve the following pair of linear equations by graph method. 2x + y = 6 and 2x – y + 2 = 0. (J’18)
- Solve the equations by graphically 3x + 4y = 10 and 4x – 3y = 5. (M’19)
- Sum of the present ages of two friends are 23 years, five years ago product of their ages was 42. Find their ages 5 years hence. (M’19)
- Draw the graph of x + y = 11 and x – y = 5. Find the solution of the pair of linear equations (J’19)
5.QUADRATIC EQUATIONS
1 Marks
- Check whether 1 and 3/2 are the roots of the equation 2x2 – 5x + 3 = 0. (J’15)
- If b2 – 4ac > 0 in ax2 + bx + c = 0, (a ≠ 0); then what can you say about roots of the equation? (M’16)
- Find the value of k, if 2 is one of the roots of the quadratic equation x2 – kx+ 6 = 0 (J’16)
- Write the nature of roots of the quadratic equation 2x2– 5x + 6 = 0 (M’17)
- Write the nature of the roots of the quadratic equation x2 – 8x + 16 = 0. ( J’17)
- Find sum and product of the roots of the quadratic equation x2– 4√3x + 9 = 0. (M’18)
- Find the values of k for which the quadratic equation 4x2 + 5kx + 25 = 0 has equal roots. (J’18)
- Find the roots of the quadratic equation x2 + 2x – 3 = 0. (M’19)
- Find the discriminant of the quadratic equation 3x2 – 5x + 2 = 0 and hence write the nature of its roots. (J’19)
- Is (x + 2)2 = x2 + 3 a Quadratic Equation? Justify. (May 2022)
- Is x (2x + 3) = x2 + 5 is a Quadratic Equation? Justify (Aug 2022)
- Solve the quadratic equation 2sin2 θ – 3 sin θ + 1 = 0 where 0° < θ ≤ 90°. (Apr’23)
2 Marks
- If 9x2 + kx + 1 = 0 has equal roots, then find the value of k. (M’16)
- The sum of a number and its reciprocal is 10/3 Find the number. (M’17)
- Is it possible to design a rectangular Garden, whose length is twice of its breadth and area is 200 m2? If so, so find its length and breadth. ( J’17)
- If the equation kx2–2kx + 6 = 0 has equal roots, then find the value of k. (M’18)
- Without calculating the roots of x2 – 5x + 6 = 0, explain the nature of roots. (J’18)
- Write the Quadratic equation, whose roots are 2 + √3 and 2 – √3 . (M’19)
- Find the roots of quartic equation x2 + 4x + 3 = 0 by “completing square method”. (J’19)
- Shashanka said that (x + 1)2 = 2(x – 3) is a quadratic equation. Do you agree? (J’19)
- Write a Quadratic Equation, whose roots are 2 – √3 and 2 + √3 .(Aug 22)
4 Marks
- If the sum of the areas of two squares is 468m2 and the difference of their perimeters is 24m., then find the measurements of their sides. (J’15)
- Sum of the squares of two consecutive positive even integers is 100; find those numbers by using quadratic equations. (M’16)
- If – 4 is a common root for the quadratic equations 2x2 + px + 8 = 0 and p (x2 + x) + k = 0 (J’17)
- Sum of squares of two consecutive even numbers is 580.Find the numbers by writing a suitable quadratic equation. (M’18)
- If a number when increased by 12, equals 160 times of its reciprocal, then find the numbers.(J’18)
- Sum of the areas of two squares is 850 m2. If the difference of their perimeters is 40 m. Find the sides of the two squares. (M’19)
- A train travels 360 km. at a uniform speed. If the speed had been 5 km./h more, it would have taken 1 hour less for the same journey. Find the speed of the train. (J’19)
- The numerator of a fraction is 3 less than its denominator. If 2 is added to both numerator and denominator, the sum of the new fraction formed and original fraction is 29/20 then find the original fraction. (Jun’23)
6.PROGRESSIONS
1 Mark
- The hand- bore well dealer charges Rs 200/- for the first one meter only and raises drilling charges at the rate of rupees 30/- for every subsequent meter. Write a progression for the above data. (M’15)
- In a flower garden, there are 23 plants in the first row, 21 plants in the second row,19 plants in the third row and so on. If there are 10 rows in that flower garden, then find the total number of plants in the last row with the help of the formula tn = a + (n – 1) d. (M’15)
- Write the common difference of an Arithmetic Progression, whose nth term is given by tn = 3n + 7. (J’15)
- Find the sum of first 200 natural numbers. (M’16)
- Is ‘zero’ is a term of the Arithmetic Progression 31, 28, 25, . .? Justify your answer. (J’16)
- In a G.P. tn = (–1) n.2017. Find the common ratio. (M’17)
- The nth term of AP is 6n + 2. Find the common difference (n∈ N) ( J’17)
- The sequence √3 , √6 , √9 , √12, . . . form an Arithmetic Progression? Give reason. (M’18)
- For the A.P. :–3, –7, –11,………. ; can we find directly a30 – a20 without actually finding a30 and a20. ( J’18 )
- Radha says “1, 1, 1,…………. are in A.P. and also in G.P”. Do you agree with Radha? Give reason. (M’19)
- Find the 11th term of the A.P. : 15, 12, 9,……….. (J’19)
- Find the 10th term of the arithmetic progression 3, 5, 7,…….. (May 2022)
- Find the 10th term of an arithmetic progression 5, 9, 13, . . . .
2 Marks
- If 7 times of 7th term of an Arithmetic Progression is equal to the 11 times of 11th term of it, then find the 18th term of that Arithmetic Progression. (J’15)
- Measures of sides of a triangle are in Arithmetic Progression. Its perimeter is 30 cm., the difference between the longest and shortest side is 4 cm; then find the measures of the sides. (M’16)
- Explain the tops in the formula Sn= n/2 [2a + (n − 1)d] ( J’16)
- Find the sum of the first 10 terms of an A.P. 3, 15, 27, 39,………….. (M’17)
- Find the value of ‘k’ so that k + 2, 4k – 6 and 3k – 2 are the three consecutive terms of an A.P. ( J’17)
- Find the 7th term from the end of the automatic progression 7, 10, 13,….. 184. (M’18)
- In a rangoli design of 13 rows, every row increases its previous row by two dots and first row contains 5 dots, then how many total dots are in the design? ( J’18 )
- Write the formula of nth term of G.P. and explain the terms in it. (M’19)
- Which term of the G.P. :√2 , 2, 2√2 , 4, . . . . . . . . . . . . is 32. ( J’19)
- 5, 8, 11, 14,……….. is an arithmetic progression. Find the sum of first 20 terms of it. (May 22)
- 3, 6, 9, 12,………… is an arithmetic progression. Find the sum of first 20 terms of the progression. (Aug.22)
- Which term of the A.P. 21, 18, 15,… is – 81? Also find the term which becomes zero. (Apr’23)
- If 6 times of 6th term of an arithmetic progression is equal to 9 times of 9th term of it, then show that 15th term of that A.P. is zero. (Jun’23)
4 Marks
- If the sum of the first 7 terms of an Arithmetic Progression is 49 and that of first 17 terms is 289, then the first ‘n’ terms. (M’15)
- A manufacturer of TV sets produced 500 sets in the third year and 700 sets in the seventh year.Assuming that the production increase uniformly by a fixed number every year. Find the production of TV sets in the 15th year the total production of TV sets in the first 10 years. (J’15)
- Find the sum of all the three digit numbers as, which are divisible by 4. (M’16).
- The sum of the three terms which are in in an arithmetic progression is 33. if the product of the first and the third terms exceeds the second term by 29, find the Arithmetic Progression. (J’16)
- Find the sum of all three-digit natural numbers, which are divisible by 3 and not divisible by 6. (M’17)
- The sum of 5th and 9th terms of A.P. is 72 and the sum of 7th and 12th terms is 97. Find the A.P. (J’17)
- Which term of G.P.: 3, 9, 27, . . . . . . . is 2187? (J’17)
- Find the sum of all two-digit odd positive integers which are divisible by 3 but not by 2. (M’18)
- Find the sum of the integers between 100 and 500 that are divisible by 9. ( J’18 )
- Find the sum of all two-digit odd multiples of 3. (M’19)
- Find the sum of all integers the between 1 to 50 which are not divisible by 3. (J’19)
7.COORDINATE GEOMETRY
1 Marks
- Find the centroid of a triangle, whose vertices are (3, 4), (–7, –2) and (10, –5). (M’15)
- Find the distance between the points (0, 0) and (a, b). (J’15)
- Find the midpoint of the line segment joining the points (–5, 5) and (5, –5). (M’16)
- If the slope of the line passing through the two points (2, 5) and (5, 8) is represented by tan θ ; (where 00 < θ < 900) in trigonometry, then find angle ‘θ’ (J’16)
- A(0, 3), B(k, 0) and AB = 5. Find the positive value of k. (M’17)
- Find the distance between the points (1, 5) and (5, 8). (M’18)
- What is the other end of the diameter of the circle, who’s the centre is (1, 2) and one end point of the diameter is (3, 4)? ( J’18 )
- Find the centroid of a ∆PQR, when vertices are P(1, 1), Q(2, 2), R(–3, –3). (M’19)
- Determine ‘x’ so that 2 is the slope of the line passing through A(– 2, 4) and B(x, –2). (J’19)
- Find the distance between the points (0, 0) and (sin θ, cos θ), where (0o ≤ θ ≤90o). (May 2022)
- Find the distance between the points (sec θ, 0) and (0, tan θ) when θ = 45° (Aug.22)
- Find the centroid of the triangle whose vertices are (2, 3), (-4, 7) and (2, – 4). (Apr.23)
2 Marks
- Show that the points A(4, 2), B(7, 5) and C(9, 7) are collinear. (M’15)
- A(3, 6),B (3, 2) and C(8, 2)are the vertices of a rectangle ABCD. Plot these points on a graph paper. From this find the co-ordinates of vertex D, so that ABCD will be a rectangle. (J’15)
- Show that the points A (–3, 3) B(0, 0) C(3, –3) are collinear. (M’16C)
- The distance between the points (8, x) and (x, 8) is 2√2 units, then find the value of x.(J’16)
- Two vertices of a triangle are (3, 2), (–2, 1) and its centroid is ( 5/3, −1/3) Find the third vertex of the triangle. (M’17)
- Find the angle made by the line joining (5, 3) and (–1, – 3) with the positive direction of X – axis. (M’17)
- Determine ‘x’, if the slope of the line joining the two points (4, x), (7, 2) is 8/3 ( J’17)
- In the diagram on a lunar eclipse, the positions of the sun, earth and moon are Shown by (–4, 6) buy, (k, –25) and (5, –6) respectively, then find the value of k. (M’18)
- Find the coordinates of the point divide the segment joining (2, 3) and (– 4, 0) in 1: 2.( J’18 )
- Akhila says, “points A(1, 3), B(2, 2), C(5, 1) are collinear”. Do you agree with Akhil? Why? (M’19)
- If the area of the triangle formed by joining the points A(x, y) B (3,2) and C(- 2, 4) is 10 square units, then show that 2x + 5y + 4 = 0 (Jun’23)
4 Marks
- Name the type of quadrilateral formed by joining the points A(–1, –2), B(1, 0), C(–1, 2) and D(–3, 0) on a graph paper. Justify your answer. (M’15)
- If A (–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, then find the area of the quadrilateral ABCD. (J’15)
- Find the co-ordinates of the points trisection of the line segment joining the points (–3, 3) and (3, –3) (M’16)
- If the points P(– 3, 9), Q(a, b) and R(4, – 5) are collinear and a + b = 1, then find the values of a and b. (J’16)
- The points C and D on the line segment joining A(–4, 7) and B(5, 13) Such that AC = CD = DB. Then find the co-ordinates of point C and D. (M’17)
- The area of the triangle is 18 sq. units, whose vertices are (3, 4), (–3, –2) and (p, –1); then find the value of ‘p’. ( J’17)
- Find the points of trisection of the line segment joining the points (–2, 1) and (7, 4). (M’18)
- Show that the points A (–1 ,–2), B (4, 3), C (2, 5) and D ( –3, 0) in that order form a rectangle. ( J’18 )
- Find the ratio in which X – axis divides the line segment joining the points (2, –3) and (5, 6). Then find the intersecting point on X – axis. (M’19).
- Find the area of the Rhombus ABCD, whose vertices are taken in order, are A (–1,1), B(1, –2), C(3, 1), D(1, 4). (J’19).
- Show that the distance of the points (5, 12), (7, 24) and (35, 12) from the origin are arranged in ascending order forms an arithmetic progression. Find the common difference of the progression. (May 2022)
- Show that the distance of the points (5,12), (7, 24) and (35, 12) from the origin are arranged in the ascending order, forms and arithmetic progression. Find the common difference of the progression.
- If A(- 2, 2) B(a, 6) C(4,b) and D(2, – 2) are the vertices of a parallelogram ABCD, then find the values of a and b. Also find the lengths of its sides. (Apr’23)
- Show that the quadrilateral formed by joining the points (-4, 2), (4, 4), (2, 12) and (-6, 10) taken in order is a square. (Jun’23)
8.SIMILAR TRIANGLES
1 Mark
- In a ∆DEF; A, B and C are the mid-points of EF, FD and DE respectively. If the area of ∆DEF is 14.4cm2, then find the area of ∆ABC. (M’15)
- In a ∆PQR and ∆XYZ, it is given that ∆PQR ∼∆XYZ, ∠Y +∠Z= 900 and XY : XZ = 3 : 4. Then find the ratio of sides in ∆PQR. (J’15)
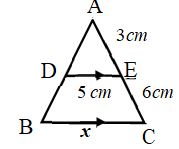
- In the given figure, ∆ABC ∼∆ADE, then find the value of ‘x’. (M’16)
- 4. It is given that ∆ABC∼∆DEF. is it true to say that BC /CD= AB/EF ? Justify your answer. (J’16)
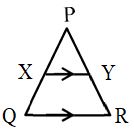
- 5. Draw the diagram corresponding to basic proportionality theorem. (J’17)
- 6. Srivani walks 12 m due to East and turns left and walks another 5 m, how far is she from the place she started? (M’18)
- 7. Write the similarity by criterion by which pair of triangles are similar (M’19)
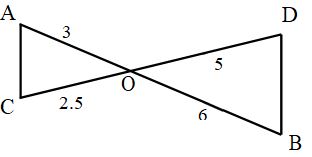
- 8. Madhavi said “All squares are similar”. Do you agree with her statement? justify your answer. (J’19)
- 9. Draw a line segment of length 7.3 cm and divide it it in the ratio 3 : 4. (J’19)
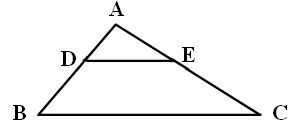
- 10. In the given figure, ABC is a triangle. AD = 3 cm, DB = 5cm, AE = 6 cm and EC = 10 cm. Is DE ⃦ BC? Justify. (May 2022)
- 11. The sides of a triangle measure 2√2 , 4 and 2√6 units. Is it a right-angled triangle? Justify. (Apr’23)
- 12. In ABC, DE is a line such that AD = 3 cm , AB = 5 cm, AE = 6 cm and AC = 10 cm. Is DE || BC ? Justify (Jun’23)
2 MARKS
- A ladder of 3.9 m length is laid against a wall. The distance between the foot of the wall and the ladder is 1.5 m. find the height at which ladder touches the wall. (M’15)
- AB is a chord of the circle and AOC is its diameter, such that ∠ACB = 600. If AT is the tangent to the circle at the point A, then find the measure of ∠BAT. (J’16)
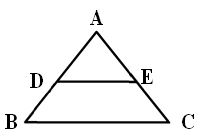
- Observe the below diagram and find the values of x and y. (M’15)
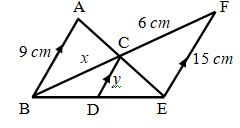
- 4. Observe the below figure. In a ∆PQR, if XY∥ QR and PX = x– 2, XQ = x + 5, PY = x – 3 and YR = x + 3, then find the value of ‘x’. (J’15)
5. ABC is an isosceles triangle and ∠B = 900, then show that AC2 = 2AB2. (M’16)
6. In DABC, PQ ‖ BC and AP = 3x– 19, PB = x– 5, AQ = x– 3, QC = 3 cm. Find x. (M’18)
7. In ABC, D and E are points on AB and AC respectively. If AB = 14 cm; AD = 3.5 cm, AE = 2.5 cm and AC = 10 cm, show that DE ‖ BC. (J’18)
8. If the ratio of areas of two equilateral triangles is 25 : 36, then find the ratio of heights of the triangles. (J’19)
4 Marks
- Construct a triangle of sides 5cm, 6cm and 7cm then construct a triangle similar to it, whose sides are 2/3 of the corresponding sides of the first triangle. (M’16)
- Construct a triangle of sides 5cm, 6cm and 7cm. then construct a triangle similar to it, whose sides are 1 1/2 times the corresponding sides of the first triangle. (J’16)
- Construct an equilateral triangle XYZ of side 5 cm and construct another triangle similar to triangle XYZ, each of its sides is 4/5 of the sides of DXYZ. (M’18)
- Construct a triangle ABC in which AB = 5 cm, BC = 7 cm and angle B = 500, then construct 4/5 a triangle similar to it, whose sides are of the corresponding sides of first triangle. (J’18)
- Construct a triangle PQR, in which PQ = 4 cm, QR = 6 cm and ∠PQR = 700. Construct triangle such that each side of the new triangle is 3/4 of the triangle PQR. (M’19)
- In a right-angle triangle, the hypotenuse is 10 cm more than the shortest side. If third side is 6 cm less than the hypotenuse, find the sides of the right-angle triangle. (M’19)
- In a right-angle triangle, length of the hypotenuse is 6 cm more than its shortest side. The length of the other side is 3 cm less than the hypotenuse, then find the sides of right-angle triangle. (J’19)
- Construct triangle ABC with BC = 7cm, angle B = 45 deg and angle C = 60°. Then construct another triangle similar to ΔABC, whose sides are 3/5 times of the corresponding sides of ΔABC. (Apr’23)
9.Tangents and Secants to The circles
1 Marks
- How many tangents can be drawn to a circle from a point on the same circle ?justify your answer. (M’15)
- Find the length of the tangent from a point, which is 9.1cm away from the centre of the circle, whose radius is 8.4cm. (J’15)
- The length of the tangent from an external point ‘P’ to a circle with center ‘O’ is always less than ‘OP’. Is this statement true? Give reasons. ((J’16)
- The length of the minute hand of a clock is 3.5 cm. Find the area swept by minute hand in 30 minutes.( use π = 22/7 ) (M’17)
- The length of the tangent to a circle from a point 17 cm from its Centre is 18 cm. Find the radius of the circle. (M’18)
- Find the length of the tangent to circle from a point 13 cm away from the centre of the circle of radius 5 cm. (J’18)
- A point P is 25 cm from the centre O of the circle. The length of the tangent drawn from P to the circle is 24 cm. Find the radius of the circle. (M’19)
4/6 Marks
- Draw a circle with radius 3cm and construct a pair of tangents from a point 8cm away from the centre. (M’15)
- Draw a circle of radius 5cm. from a point 8cm away from its centre, construct a pair of tangents to the circle. Find the lengths of tangents. (M’16)
- Two concentric circles of radii 10cm and 6cm are drawn. Find the length of the chord of the larger circle which touches the smaller circle. ((J’16)
- Draw a circle of diameter 6 cm from a point 5 cm away from its centre. Construct the pair of tangents to the circle and measure their length. (M’17)
- Draw two concentric circles of radii 1.5 cm and 4 cm. From a point 10 cm from its centre, construct the pair of tangent to the circle. (J’17)
- Draw a circle of radius 6 cm and construct two tangents to the circle so that angle between the tangents is 60°. (J’19)
- Draw a circle of radius 4 cm. From a point 9 cm away from it’s centre, construct a pair of tangents to the circle. (May 2022)
- Draw a circle of radius 4 cm. From a point 9 cm away from it’s centre, construct a pair of tangents to the circle.(Aug.22)
- Construct a circle of radius 5 cm. Then construct a pair of tangents to the circle such that the angle between them is 60°,(Jun’23)
10.MENSURATION
1 Marks
- If a cylinder and a cone are of the same radius and height ,then how many cones full of milk can fill the cylinder? Answer with reasons. (M’15)
- If the radius of hemisphere is 21cm, then find its volume. (J’15)
- “A conical solid block is exactly fitted inside the cubical box of side ‘a’, then the volume of
- conical solid block is 4/3 π a3 ”. Is this statement true? Justify your answer. (M’16)
- If the surface area of a hemisphere is ‘S’, then express ‘r’ in terms of ‘S’. (M’16)
- Find the curved surface area of a cylinder of radius 14cm and height 21cm.(π =22/7 ) (J’16)
- Write the formula to find curved surface area of a cone and explain each term in it. (M’17)
- If a cone is inscribed in a cylinder, what is the ratio of their volumes? (J’17)
- The vertex angle of a cone is 600. Find the ratio of the diameter with the height of the cone.
- “cuboid is one of right prism’. Is it true? Justify. (J’17)
- Write the formula to find the volume of a cone and explain each term in it. (J’18)
- Find the value of liquid hemispherical bowl can hold, where radius of the ball is 4.2 cm. (J’18)
- In a hemispherical bowl of 2.1 cm radius ice-cream is there. Find the volume of the bowl.(M’19)
- If the metallic cylinder of height 4 cm and radius 3 cm is melted under recast into a sphere, then find the radius of the sphere. (J’19)
- Write the formula for finding lateral surface area of a cylinder and explain each term in it. (J’19)
- A joker cap is in the form of a right circular cone, whose base radius is 7 cm and slant height is 25 cm. Find it’s curved surface area. (May 2022)
- If the ratio of a base radii of two right circular cylinder is 1:2 and the ratio of their heights is 2:3 then find the ratio of their values. (Aug.22)
2 Marks
- The radius of a spherical balloon increases from 7cm to 14 cm as air pumped into it. Find the ratio of the volumes of the balloon before and after pumping the air. (M’15)
- Find the volume and surface area of a sphere of radius 42cm (π =22/7 ) (M’16)
- A solid metallic ball of volume 64cm3 melted and made into a solid cube. Find the side of the solid cube. (M’16)
- A toy is in the form of a cone mounted on a hemisphere. The radius of the base and the height of the cone are 7cm and 8cm respectively. Find the surface area of the toy. (J’16)
- The diameter of a solid sphere is 6 cm. It is melted and recast into a solid cylinder of height 4
- cm. Find the radius of cylinder. (M’17)
- The height and the base radius of a Cone and a Cylinder are equal to the radius of a Sphere. Find the ratio of their volumes. (M’18)
- The diameter of the base of a right circular cone is 12 cm and volume 376.8 cm3. Find its height (π = 3.14) (J’18)
- A right circular cylinder has radius 3.5 cm and height 14 cm. Find curved surface area. (M’19)
4 Marks
- A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. If the length of the cylindrical part of the capsule is 14mm and the diameter of hemisphere is 6mm, then find the volume of medicine capsule. (M’15)
- The area of a sector-shaped canvas cloth is 264m2. With this canvas cloth, if a right circular conical tent is erected with the radius of the base as 7m, then find the height of the tent.(J’15)
- DWACRA is supplied cuboidal shaped wax block with measurements 88cm x 42cm x 35cm. from this how many number of cylindrical candles of 2.8cm diameter and 8cm of height can be prepared? (M’16)
- How many spherical balls each 7cm in diameter can be made out of a solid lead cube whose edge measures 66cm? (J’16)
- The length of a cuboid is 12 cm, breadth and height are equal in measurements, and its volume is 432 cm3. The cuboid is cut into two cubes. Find the lateral surface area of each cube. (M’17)
- How many silver coins of diameter 5 cm and thickness 4 mm have to be melted to prepare a
- cuboid of 12 cm X 11 cm X 5 cm dimension? (M’18)A metallic sphere of diameter 30 cm is melted and recast into a cylinder of radius 10 cm. Find the height of the cylinder. (J’18)
- A toy is made with seven equal cubes of sides√7cm. Six cubes are joined to six faces of a seventh cube. Find the total surface area of the toy. (M’19)
- A cylindrical tank of radius 7 m has water to some level. If 110 cubes of the side off the side 7 cm are completely measured in it, then find the raise in water level. (J’19)
- The sum of the radius of base and height of a solid right circular cylinder is 37 cm. if its total surface area is 1628 cm2, then find the volume of the cylinder(Use π = 22/7 )(May’ 2022)
- A metallic vessel is in the shape of a right circular cylinder mounted over a hemisphere. The common diameter is 42 cm and the height of the cylindrical part is 21 cm. Find the capacity of the vessel. (Take π = 22/7 ). (Aug’ 2022)
11.TRIGONOMETRY
1 Mark
- Show that tan28 – 1/Cosec2θ= –1. (M’15)
- Explain the meaning of cos A. (J’15)
- If tan 8 = √3 (where 8 is acute), then find the value of 1 + cos 8. (M’16)
- Evaluate :sin 580/cos 320 + tan 420/cot 480. (J’16)
- If Sin A = 1/√2 and cot B = 1, prove that sin (A + B) = 1, where A and B are both are acute angles. (M’17)
- Express cosθ in terms of tanθ . (M’17)
- If cosθ = 1/√2, then find the value of 4 + cotθ. (M’17)
- Is it correct to say that sinθ = cos (90 – θ) why? (J’17)
- Find the value of tan 2A, if cos 3A = sin 450. (M’18
- Prove that 4 tan2450 – cosec2300+ cos2300=4 (J’18)
- Evaluate cosec 390 .sec 510 – tan 510 . cot 390. (M’19)
- In a right triangle ABC, right angled at ‘C’ in which AB = 13 cm, BC = 5 cm, determine the value of cos2 B + sin2 A. (M’19)
- Ravi says “the value of tan 00.tan10.tan20. . . . . . .. . . . . . .tan890 is zero”. Do you agree with Ravi? Give reason. (J’19)
- Express tan θ in terms of sin θ. (May 22)
- Express sec θ in terms of sin θ. (Aug 22)
- Express ‘tan θ’ in terms of ‘sin θ’. (Apr’ 23)
- Express ‘tan θ’ in terms of ‘cos θ’. (Jun’23)
2 Marks
- Show that (1 + cot2 8) (1 – cos 8) (1 + cos 8) = 1 . (M’15)
- Show that √sec28 + cosec28 = tan8 + cot 8. (J’15)
- Prove that √1–sin 8/1+sin 8= sec8 – tan 8, (where 8 is acute). ((M’16)
- If tan (A + B) = 1 and cos (A – B) =√3/2, 00 < A+B < 900 and A > B; find A and B. (M’16)
- If x = a secθ and y = b tanθ, then prove that x2/a2 – y2/b2 = 1. ((J’16)
12.APPLICATIONS OF TRIGONAMETRY
1 Mark
- A person from the top of a building oh height 25m has observed another building’s top and bottom at an angle of elevation of 450 and at an angle of depression 600 respectively. Draw a diagram for this data. (M’15)
- A person observed the top of a tree at an angle of elevation of 600 when the observation point was 5m away from the foot of the tree. Draw a diagram for this data. (J’15)
- “If the angle of elevation of Sun increases from 00 to 900, then the length of a tower decreases”, is this statement true? Justify your answer. ((M’16)
- If a tower of height ‘h’ is observed from a point with a distance ‘d’ and angle ‘8’, then express the relation among h, d and 8. (J’16)
- A pole and its shadow have same length, find the angle of the ray male with the earth at that time. (M’18)
- An observer observes the top of a tower from two points on the same side of a tower and on the same straight line which are at distances of 5 m and 8 m with angles of elevation 60° and 45° respectively. Draw a suitable diagram for the given data. ( Aug.22)
- .”An observer standing at a distance of 10m from the foot of a tower, observes its top with an angle of elevation of 60° ”. Draw a suitable diagram for this situation. ( Apr’.23)
2 Marks
- A boat has to cross a river. It crosses the river by making an angle of 600 with the bank of the river due to stream of the river and travels a distance of 450m to reach the another side of the river. Draw the diagram for this data. (M’16)
- A person 25 m away from a cell tower observes the top of the cell tower at an angle of elevation 30°. Draw the suitable diagram for this situation. (M’17)
- A State highway a leads to foot of the tower. A Man Standing at the top of the tower observes a car at an angle of depression of θ , which is approaching to the foot of the tower with a uniform speed. 6 seconds later the angle of depression is $. Draw a diagram for this data and analyze. (J’17)
- From the top of the tower of height h m height, Anusha observes the angles of depression of two points X and Y on the same side of the tower on the ground to be α and þ. Draw the suitable figure for the given information. (M’18)
- The angle of elevation of the top of a tower from a point on the ground, which is 50m away from the foot of the tower, is 450. Draw the diagram for the situation. (J’18)
- From the top of the building the angle of elevation of the top of the cell tower is 600 and the angle of depression to its foot is 450, if the distance of the building from the tower is 30m, draw the suitable diagram to the given data. (M’19)
- From the top of the building, The angle of elevation of the top of a TV tower is and the angle is α0 and the angle of depression to its (T.V. tower) foot is þ0 . if distance of the building from the tower is ‘d’ metres, draw the suitable diagram of the given data.(J’19)
- The statue stands on the top of 3 m tall pedestal. From a point on the ground angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the statue.(Aug.22)
4 Maks
- An observer flying in an latitude of 900m observes two ships in front of him, which are in the same direction at an angles of depression of 600 and 300 respectively. Find the distance between the two ships. (M’15)
- A person from the top of a building of height 15meters observes the top and the bottom(foot) of a cell tower with the angle of elevation as 600 and the angle of depression as 450 respectively. Then find the height of the cell tower. (J’15)
- Two poles of equal heights are standing opposite to each other, on either side of the road, which is 80m wide. From a point between them on the road, the angles of elevation of top of the poles are 600 and 300 respectively. Find the height of the poles. (M’16)
- A tree is broken without separating from the stem by the wind. The top touches the ground making an angle 300 at a distance of 12m from the foot of the tree. Find the height of the tree before breaking. (J’16)
- Two poles are standing opposite to each other on the either side of the road which is 90 feet wide. The angle of elevation from bottom of the first pole to the top of the second Pole is 450.The angle of elevation from the bottom of the second pole to the top of the first pole is 30°. Find the heights of the poles. (use √3 = 1.732) (M’17)
- The angle of elevation of top of the tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same to straight line with it, are complementary. Prove that the height of the tower is 6 m. (J’17)
- From the top of a tower of 50m high, Neha observes the angles of depression of the top and foot of another building to be 45° and 60° respectively. Find the height of the building.(M’18)
- Two boys on either side of their school building of 20 m height observes its top at the angles of elevation 30° and 60° respectively. Find the distance between two boys. (J’18)
- The angle of elevation of the top of a hill from the foot of a tower is 600 and the angle of elevation of the top of the tower from the foot of the hill is 300. If the tower is 50 m high. Find the height of the hill. (M’19)
- A man observes top of tower at an angle of elevation of 30°. When he walked 40 m towards the tower, the angle of elevation is changed to 600. Find the height of the tower and distance from the first observation point to the tower. (J’19).
- If two persons standing on either side of a tower of height 100 metres observes the top of it with angles of elevation of 60o and 45o respectively, then find the distance between the two persons. (May 2022)
- If two boys standing on either side of their school building of height 20m, observed the top of it with angles of elevation of 30° and 60° respectively, then find the distance between the two boys. (Jun’23)
13.PROBABILITY
1 Mark
- When a die is rolled once unbiased, what is the probability of getting a multiple of 3 out of possible outcomes? (M’15)
- The probability of an event is always in between 0 and 1 why? (J’15)
- Find the probability of getting a sum of the numbers on them is 7, when two dice are rolled at a time. ((M’16)
- Find the probability of getting a prime number, when a card drawn at random from the numbered cards from 1 to 25. (J’16)
- From the first 50 natural numbers, find the probability of randomly selected number is a multiple of 3. (M’17)
- A dice is thrown once. Find the probability of getting a composite number. (J’17)
- What is the probability of getting exactly 2 heads, when three coins are tossed simultaneously. (M’18)
- When a dice is rolled, find the probability of getting on odd prime number.(J’18)
- From English alphabet if a letter is chosen at random, then find the probability that the letter is a consonant. (M’19)
- Write two examples for equally likely events. (J’19)
- If a dice rolled once, then find the probability of getting an odd number. (May 2022)
- If an unbiased dice is rolled once, then find the probability of getting a prime number on its top face. (Aug22)
- Find the probability of getting a ‘vowel’ if a letter is chosen randomly from the word “INNOVATION” (Apr’23)
2 Marks
- There are 12 red balls, 18 blue balls and 6 white balls in a box. When a ball is drawn at random from the box, what is the probability of not getting a red ball? (M’15).
- When a card is drawn from a well shuffled deck of 52 cards, then find the probability of NOT getting a red faced card. (J’15)
- There are 5 red balls, 4 green balls and 6 yellow balls in a box. If a ball is selected at random, what is the probability of not getting a yellow ball? ((J’16)
- What is the probability of a number picked from first 20 natural numbers is even composite number? (M’18)
- A bag contains 7 red, 5 white it and 6 black balls. A ball is drawn from the bag at random; find the probability that the ball drawn is not black.(J’18)
- A bag contains balls which are numbered from 1 to 50. A ball is drawn at random from the bag, the probability that it bears two digit number multiple of 7. (M’19)
- A box contains 4 red balls, 5 green balls and P white balls. If the probability of randomly picked a ball from the box to be read ball is 1/3, then find the number of white balls. (J’19)
- A bag contains 5 red, 8 white, 4 green colour balls. If a ball is selected randomly from the bag then find the probability that selected ball is (i) a green ball (ii) not white ball.
- A box contains four slips numbered 1, 2, 3, 4 and another box contains five slips numbered 5, 6, 7, 8, 9. If one slip is taken randomly from each box,
- i) How many number pairs are possible?
- ii) What is the probability of both being odd?
- iii) What is the probability of getting the sum of the numbers 10? (Apr’23)
- If one card is randomly selected from a well shuffled deck of cards, then find the probability of getting-
- i) a face card, (ii)a jack of hearts and (iii) an ace card. (Jun’23)
- From the following data, Find the probability of selecting “B” blood group student. (J’17)
| Blood Group | A | B | AB | O |
| Number of students | 10 | 13 | 12 | 5 |
4 Marks
- There are 100 flash cards labeled from 1 to 100 in a bag. When a card is drawn from the bag at random, what is the probability of getting……..
- i) A card with prime number from possible outcomes
- ii) A card without prime number from possible outcomes. (M’15).
- A shopkeeper has 100 memory cards in a box. Among them, 15 memory cards are defective. When a person came to the shop to buy a memory card, the shopkeeper drew a memory card at random from the box. Then
- What is the probability that this memory card is defective?
- After drawing the first memory card which is defective, it is not placed back in the box. Then another memory card is drawn at random. What is the probability that this memory card is NOT defective? (J’15)
- A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of red ball, find the number of blue balls in the bag. (M’16)
- Two dice are rolled at same time and the sum of the numbers appearing on them is noted. Find the probability of getting each sum, from 3 to 5 separately. (J’16)
- A bag contains some square cards. A prime number between 1 and 100 has been written on each card. Find the probability of getting a card that the sum of the digits of a prime number written on it, is 8. (M’17)
- From the Deck of 52 cards, if a what is randomly chosen, find the probability of getting a card with (i) a prime number on it, ( ii ) face on it. (M’18)
- If two dice are thrown at the same time, find the probability of getting sum of the dots on top is prime. (M’19)
- From a pack of 52 playing cards, Jacks, Queens, Kings and Aces of red colour are removed. From the remaining, a chord is drawn at random. Find the probability that the card drawn is (i) a block queen, (ii) a red card. (J’19)
- A box contains 20 cards which are numbered from 1 to 20. If one card is selected at random from the box, find the probability that it bears (i) a prime number, (ii) an even number. (May 2022)
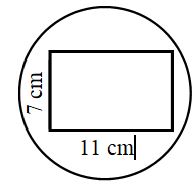
- Suppose you drop a dies at random on the circular region of diameter 28 cm as shown in the figure. What is the probability that it will land inside the rectangle.
14.STATISTICS
1 Mark
| Class Interval | 10 – 25 | 25 – 40 | 40 – 55 | 55 – 70 | 70 – 85 | 85 -–100 |
| Frequency | 2 | 3 | 7 | 6 | 6 | 6 |
- How do you find the deviation from the assumed mean for the above data? (M’15)
- Write the formula to find the median of a grouped data and explain each term. (M’16, Aug’22, A’23)
- When an observation in a data is abnormally more than or less than the remaining observations in the data, does it affect the mean or mode or median? Why? (J’15)
- Write the formula to find the mean of a grouped data, using assumed mean method and explain each term. (J’16)
- “The median of observations, – 2, 5, 3, – 1, 4, 6 is 3.5”. Is it correct? (M’17)
- Write the first 10 prime numbers and find their median. (J’17)
- Write the formula to find the median of grouped data and explain the alphabet in it. (M’18)
- Prathyusha stated that” the average of first 10 odd numbers is also 10”. Do you agree with her? Justify your answer.(M’18)
- Find the median of first seven composite numbers. (M’19) 10. Find the mode of the data 6, 8, 3, 6, 3, 7, 4, 6, 7, 3, 6. (J’19)
2 Marks
- The heights of six members of a family are given below in the table. Find the mean height of the family members. (J’15)
| Height(in ft.) | 5 | 5.2 | 5.4 | 5.6 |
| Number of Family members | 1 | 2 | 2 | 1 |
2. Find the value of fixi for the above data, where xi is the mid value of each class. (J’16)
| Class Interval | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 |
| Frequency (fi) | 5 | 8 | 10 | 5 | 2 |
3. Find a median of 2/3, 4/5,1/2, 3/4, 6/5 (M’18
4. Find the mean of prime numbers less than 30. (J’18)
5. Write the mode formula for grouped data and explain the terms in it. (J’15, M’17,19,’22, J’23)
6. Find the median of first 6 prime numbers. (J’19)
4 Marks
- In a village, an enumerator has surveyed for 25 households. The size of the family(number of family members) and the number of families is tabulated as follows:-Find the mode of the data. (M’15)
| Size of family (No. of members) | 1 – 3 | 3 – 5 | 5 – 7 | 7 – 9 | 9 – 11 |
| No. of families | 6 | 7 | 9 | 2 | 1 |
- 2. Daily expenditure of 25 householders is given in the following table :Draw a “ less than type” cumulative frequency Ogive curve for this data. (M’15)
| Daily expenditure of a family(Rs) | 100–150 | 150–200 | 200–250 | 250–300 | 300–350 |
| No. of households | 4 | 5 | 12 | 2 | 2 |
3. If the median of 60 observations given below is 28.5, then find the values of x and y. (J’15)
| Class Interval | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 |
| Frequency | 5 | x | 20 | 15 | y | 5 |
- 4. The following distribution gives the daily profits ( in rupees) earned by 50 shops in a locality. Convert the above distribution to a ‘less than type’ cumulative frequency distribution and draw its Ogive. (J’15)
| Daily Profits ( inRs.) | 0 – 50 | 50 – 100 | 100 – 150 | 150 – 200 | 200 – 250 | 250 – 300 |
| No. of shop | 6 | 9 | 13 | 10 | 8 | 4 |
- 5. Consider the following distribution of daily wages of 50 workers of a factory. (Find the mean daily wages of the workers in the factory by using step-deviation method (M’16)
| Daily wages in Rupees | 200–250 | 250–300 | 300–350 | 350–400 | 400–450 |
| No. of workers | 6 | 8 | 14 | 10 | 12 |
6. The following table gives production yield per hectare of wheat of 100 farms of a villageDraw both ogives for the above data. Hence obtain the median production yield. (M’16).
| Production Yields(Quintals/Hect.) | 50 – 55 | 55 – 60 | 60 – 65 | 65 – 70 | 70 – 75 | 75 – 80 |
| No. of farmers | 2 | 24 | 16 | 8 | 38 | 12 |
7. The scores of 20 students in a test is tabulated as follows. Find the mode of the data. (J’16)
| Marks | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 |
| No. of students | 1 | 6 | 7 | 4 | 2 |
- 8. The literacy rate (in percentage) of 35 cities is given in the following table. Prepare ‘more than type’ cumulative frequency table and draw ogive curve for this data. (J’16)
| Literacy arte % | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 | 80 – 90 |
| No. of. cities | 3 | 11 | 10 | 8 | 3 |
9. The daily wages of 80 workers of a factory,Find the mean daily wages of the workers of the factory using an appropriate method., (M’17)
| Daily wages(Rs.) | 500–600 | 600–700 | 700–800 | 800–900 | 900–1000 |
| Number of workers | 12 | 17 | 28 | 14 | 9 |
10. The following data gives the information on the observed lifespan (in hours )of 90 electrical components. Draw both ogives for the about data. (M’17)
| lives span (in hours) | 0–20 | 20–40 | 40–60 | 60–80 | 80–100 | 100–120 |
| Frequency | 8 | 12 | 15 | 23 | 18 | 14 |
- 11. Daily income of 40 coal-mine labours are given in the following table. Draw Ogive Curves (Cumulative frequency) for this data. (J’17)
| Daily Income in Rs. | 100–150 | 150–200 | 200–250 | 250–300 | 300–350 | 350 – 400 |
| Number of labours | 4 | 3 | 3 | 8 | 13 | 9 |
12. Find the missing frequencies f1 and f2 if mean of 50 observations given below is 36.4 (J’17)
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 |
| Frequency | 3 | 5 | f1 | 10 | f2 | 8 | 5 |
- 13. of the families in a locality are given. Find the mode of the data. (M’18)
| Income in Rs. | 1–200 | 201–400 | 401–600 | 601–800 | 801–1000 |
| Number of families | 7 | 10 | 16 | 12 | 3 |
14. Heights of the peoples of a particular school are given. Draw greater than compared to come and find the median height from it. (M’18)
| Height (in cm) | 90 – 100 | 100 – 110 | 110 – 120 | 120 – 130 | 130 – 140 | 140 – 150 |
| No. of Pupils | 5 | 2 | 3 | 8 | 8 | 6 |
- 15. The following table shows the ages of the patients admitted in a hospital during a year. Draw a less than ogive curve for the about data. (J’18)
| Age in years | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 |
| No. of Patients | 8 | 15 | 25 | 27 | 18 | 7 |
- 16.The below distribution gives the weight of 40 students In a class. Find the median weight of the students. (J’18)
| Weight in kg | 30 – 35 | 35 – 40 | 40 – 45 | 45 – 50 | 50 – 55 | 55 – 60 |
| No. of students | 4 | 5 | 10 | 8 | 8 | 5 |
- 17. Draw less than Ogive for the following frequency distribution. Find the median from obtained curve. (M’19)
| IQ | 60–70 | 70–80 | 80–90 | 90–100 | 100–110 | 110–120 | 120–130 |
| No. of students | 2 | 5 | 12 | 31 | 39 | 10 | 4 |
- 18. Find the mean age of 100 residents of a colony from the following data. (M’19)
| Age (in yrs) | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 |
| No. of persons | 10 | 15 | 25 | 25 | 10 | 10 | 5 |
- 19. If the mean of the following frequency distribution is 50, then find the value of k. (J’19)
| Class | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 80 | 80 – 100 |
| Frequency | 17 | 20 | 32 | k | 19 |
- 20.The following table gives the marks obtained by buy 100 students in SA – I exams in Mathematics subject. Draw ogive graph of less than and greater than. (J’19)
| Marks | 50 – 55 | 55 – 60 | 60 – 65 | 65 – 70 | 70 – 75 | 75 – 80 |
| No. of students | 2 | 8 | 12 | 24 | 38 | 16 |
- 21. Find the median for the following data. (May 2022)
| Class interval | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Frequency | 6 | 10 | 12 | 8 | 8 |
- 22. Find the mode of the following data (Aug22)
| Class interval | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 |
| Frequency | 3 | 16 | 26 | 31 | 16 | 8 |
- 23. Find the mode for the following data. (A’23)
| Class interval | 1000- 1500 | 1500- 2000 | 2000- 2500 | 2500- 3000 | 3000- 3500 | 3500- 4000 | 4000- 4500 | 4500- 5000 |
| Frequency | 24 | 40 | 33 | 28 | 30 | 22 | 16 | 7 |
- 24. Find the mode for the following data.(J’23)
| Class interval | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 |
| Frequency | 7 | 14 | 13 | 12 | 20 | 11 | 15 | 8 |
