TS 10th Class Maths Solutions
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding: (use π = 3.14)
(i) Minor segment
(ii) Major segment. (A.P. Mar. '16, June '15)
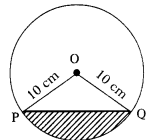
Given:
Angle subtended by the chord = 90°
Radius of the circle = 10 cm
Solution:
Area of the minor segment = Area of the sector POQ - Area of ∆POQ
Area of the sector = (x°/360°) × πr²
= (90/360) × 3.14 × 10 × 10 = 78.5 cm²
Area of the triangle POQ = ½ × Base × Height
= ½ × 10 × 10 = 50 cm²
∴ Area of the minor segment = 78.5 - 50 = 28.5 cm²
Area of the major segment = Area of the circle - Area of the minor segment
= 3.14 × 10 × 10 - 28.5
= 314 - 28.5 = 285.5 cm²
(i) Area of minor segment = 28.5 cm²
(ii) Area of major segment = 285.5 cm²
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle (use π = 3.14 and √3 = 1.732).
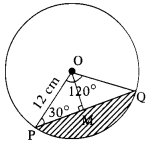
Given:
Radius of the circle r = 12 cm
Solution:
Area of the sector = (x°/360°) × πr²
Here x = 120°
= (120°/360°) × 3.14 × 12 × 12 = 150.72 cm²
Drop a perpendicular from 'O' to the chord 'PQ'
∆OPM = ∆OQM [∵ OP = OQ, ∠P = ∠Q; angles opposite to equal sides OP & OQ, ∠OMP = ∠OMQ by A.A.S]
∴ ∆OPQ = ∆OPM + ∆OQM = 2(∆OPM)
Area of ∆OPM = ½ × PM × OM
But cos 30° = PM/OP
[∴ In ∆OPQ ∠POQ = 120° ∠OPQ = ∠OQP = (180-120°)/2 = 30°]
∴ PM = 12 × √3/2 = 6√3
Also sin 30° = OM/OP
⇒ ½ = OM/12 ⇒ OM = 12/2 = 6
∴ ∆OPM = ½ × 6√3 × 6 = 18 × 1.732 = 31.176 cm²
∴ ∆OPQ = 2 × 31.176 = 62.352 cm²
Area of the minor segment PQ = (Area of the sector) - (Area of the ∆OPQ)
= 150.72 - 62.352 = 88.368 cm²
A car has two wipers which do not overlap. Each wiper has a blade of length 25cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades (use π = 22/7).
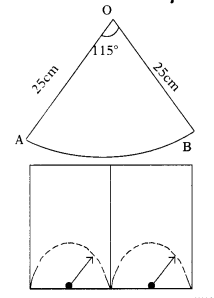
Given:
Angle made by each blade = 115°
Length of wiper blade (radius) = 25 cm
Solution:
It is evident that each wiper sweeps a sector of a circle of radius 25cm and sector angle 115°.
Area of a sector = (θ°/360°) × πr²
Total area cleaned at each sweep of the blades = 2 × (θ°/360°) × πr²
= 2 × (115°/360°) × (22/7) × 25 × 25
= 2 × (23/72) × (22/7) × 25 × 25
= (23/36) × (22/7) × 25 × 25
= 1254.96 cm²
Find the area of the shaded region in the figure, where ABCD is a square of side 10cm and semicircles are drawn with each side of the square as diameter (use π = 3.14).
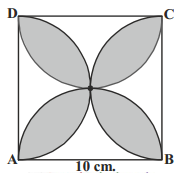
Given:
Square ABCD with side 10 cm
Solution:
Let us mark the four unshaded regions as I, II, III and IV.
Area of I + Area of III = Area of ABCD - Areas of 2 semicircles with radius 5 cm
= 10 × 10 - 2 × ½ × π × 5²
= 100 - 3.14 × 25
= 100 - 78.5 = 21.5 cm²
Similarly, Area of II + Area of IV = 21.5 cm²
So, area of the shaded region = area of ABCD - Area of unshaded region
= 100 - 2 × 21.5
= 100 - 43 = 57 cm²
Find the area of the shaded region in the figure, if ABCD is a square of side 7cm and APD and BPC are semi-circles (use π = 22/7).
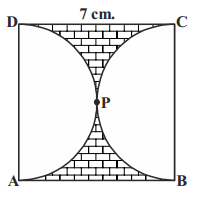
Given:
ABCD is a square of side 7 cm
Solution:
Area of the shaded region = Area of ABCD - Area of 2 semi-circles with radius 7/2 = 3.5 cm
APD and BPC are semi-circles
= 7 × 7 - 2 × ½ × (22/7) × 3.5 × 3.5
= 49 - 38.5 = 10.5 cm²
In figure, OACB is a quadrant of a circle with centre 'O' and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region (use π = 22/7).
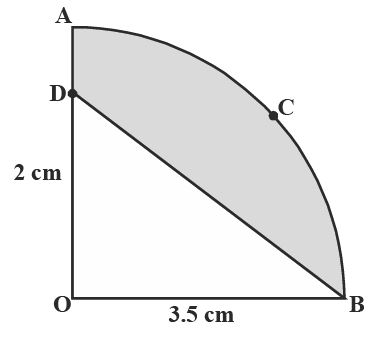
Given:
OACB is a quadrant of a circle with radius 3.5 cm
OD = 2 cm
Solution:
Area of the shaded region = Area of the sector - Area of ABOD
= (x°/360°) × πr² - ½ × OB × OD
= (90°/360°) × (22/7) × 3.5 × 3.5 - ½ × 3.5 × 2
= ¼ × (22/7) × 3.5 × 3.5 - 3.5
= ¼ × (22/7) × 12.25 - 3.5
= 9.625 - 3.5 = 6.125 cm²
AB and CD are respectively arcs of two concentric circles of radii 21cm and 7cm with centre 'O' (see figure). If ∠AOB = 30°, find the area of the shaded region (Use π = 22/7).
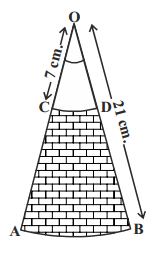
Given:
Radius of larger circle = 21 cm
Radius of smaller circle = 7 cm
∠AOB = 30°
Solution:
Area of the shaded region = Area of sector OAB - Area of the sector OCD
= (30°/360°) × (22/7) × 21 × 21 - (30°/360°) × (22/7) × 7 × 7
= (30°/360°) × (22/7) × (21 × 21 - 7 × 7)
= 1/12 × (22/7) × (441 - 49)
= 1/6 × (11/7) × 392
= 1/6 × 11 × 56
= (11 × 28)/3 = 102.67 cm²
Calculate the area of the designed region in figure, common between the two quadrants of the circles of radius 10 cm each (use π = 3.14).
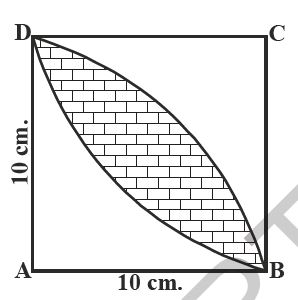
Given:
Radius of the circle (r) = 10 cm
Solution:
Area of the designed region = 2 [Area of quadrant ABYD - Area of ∆ABD]
= 2 [¼ × πr² - ½ × Base × Height]
= 2 [(¼ × 3.14 × 10 × 10) - (½ × 10 × 10)]
= 2 [78.5 - 50]
= 2 × 28.5 = 57 cm²
